Aufgabenstellung

Es wurden mir Zahlenreihen von vier verschiedenen Eigenschaften eines Produktionsprozesses zur Verfügung gestellt. Die Werte der ersten Eigenschaft bestimmen laut Angabe die Werte der anderen drei Eigenschaften. Jetzt galt es eine Formel zu finden, wie man die Werte der drei abhängigen Eigenschaften mit Hilfe der ersten Eigenschaft berechnen kann.

Es handelt sich also um ein Regressionsproblem.

Die nachfolgenden Berechnungen in R habe ich mit Hilfe der Anleitung Beispiel in R: Einfache lineare Regression von Regina Tüchler erarbeitet.

Die erste Regression

Den folgenden Code in R habe ich in der Datei Regression1.r zusammengefasst.

Zunächst werden die beiden Daten Vektoren angelegt, wobei ich den Namen y1 für die abhängige Variable und x für die Eigenschaft, aus der sich die anderen Werte errechnen lassen sollen, vergeben habe.

        x <- c(0.7, ..., 68.2);
        y1 <- c(37.35919, ..., 69.07001);
      

Danach habe ich einen ersten Plot gemacht, um mir ein Bild von der Abhängigkeit zu machen.

          plot(x, y1);
      

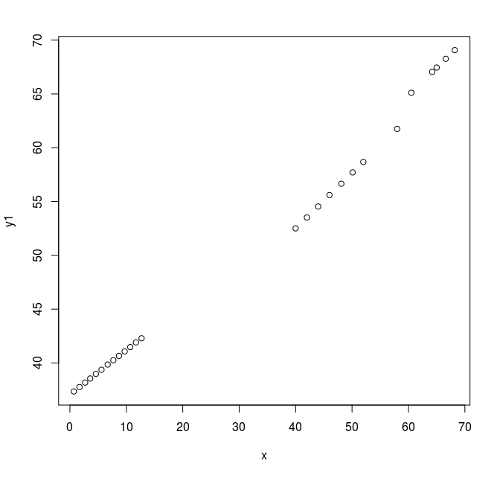
Abbildung 1: Erster Plot x gegen y1 zeigt, dass eine lineare Abhängigkeit visuell denkbar ist.

Nachdem eine lineare Abhängigkeit vom Plot her denkbar ist, habe ich mit folgendem Befehl das lineare Modell berechnen lassen:

          fmY1 = lm(y1 ~ x);
      

Mit der Eingabe von fmY1 wurden folgende Daten ausgegeben:

Coefficients:
(Intercept) x
36.5322     0.4496


Anschließend habe ich mir das maximale Residuum, also die maximale Abweichung eines Datenpunkts von der geschätzten Funktionsgeraden, mit max(abs(residuals(fmY1))) ausgeben lassen. Es wird ein Wert von 2.006533 ausgegeben.

Da ich die Vorgabe hatte eine Abweichung von unter 1 zu erhalten, habe ich danach ein quadratisches Modell erstellt. Dafür habe ich zunächst eine weitere Variable x2 mit dem quadrierten Werten von x erstellt und diese dann in das lineare Modell hinzugefügt.

          x2 = x*x;
          fmY1qu = lm(y1 ~ x + x2);
      

Dies ergab folgende Parameter für die Funktion:

(Intercept) x         x2
37.949797   0.242187  0.003169

Das maximale Residuum wurde mit max(abs(residuals(fmY1qu))) als 0.9060824 ausgegeben, was für meine Aufgabenstellung ausreichend war.

Somit konnte ich das Resultat in einer Grafik ausgeben lassen:

          plot(x, y1)
          abline(fmY1, col="red")
          lines(x, fitted(fmY1qu), col='blue') 
      

Abbildung 2: Zweiter Plot x gegen y1 und die Regressions-Ergebnisse

Aus der Abbildung kann man erkennen, dass sich die lineare Schätzung sehr stark an den ersten 13 Datenpunkten im linken unteren Quadranten des Plots konzentriert. Die nächste Punkte Serie in der Mitte bleibt unter der roten Linie, während die Punkte im rechten oberen Quadranten über der Schätzung liegen. Man bräuchte also für die lineare Schätzung mehr Datenpunkte in dem Wertebereich zwischen 20 und 30 von x oder noch mehr Daten in den höhren Bereichen, um eventuell eine bessere lineare Annäherung zu erreichen.

Die blau eingezeichnete quadratische Lösung schmiegt sich sehr schön an die gegebenen Daten an. Sie bietet für den abgebildeten Werte-Bereich sicherlich eine sehr gute Schätzung. Allerdings bleibt offen, ob die Krümmung der Kurve außerhalb des dargestellten Wertebereichs von x noch korrekt ist.

Die zweite Regression

Den folgenden Code in R habe ich in der Datei Regression2.r zusammengefasst.

Nach dem Anlegen der Vektoren x und y2 ergibt sich folgendes erstes Bild der Daten.

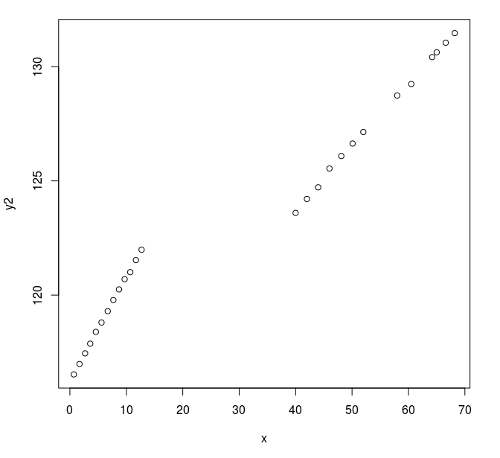
Abbildung 3: Erster Plot x gegen y2

Daraus kann man ersehen, dass es eine signifikante Sprungstelle in den Daten gibt. Dies kann durch ein lineares Modell sicherlich nicht kompensiert werden. Man könnte jetzt ein höhergradiges Modell anwenden, oder für die beiden Gruppen jeweils getrennt ein lineares Modell anwenden. Bei letzterer Variante, ist allerdings unklar, ab welchem Wert von x, zwischen den Modellen gewechselt werden soll.

Ich habe zunächst die Modelle höheren Grades mit folgenden Befehlen erstellt.

          x2 = x*x;
          x3 = x*x*x;

          fmY2 = lm(y2 ~ x);
          fmY2qu = lm(y2 ~ x + x2);
          fmY2cub = lm(y2 ~ x + x2 + x3);
      

Dies ergab folgende Werte pro Modell:

Modell	Formel	Max. Residuum
Linear	y2 = 0,1868 * x + 117,7756	1,837904
Quadratisch	y2 = 0.0008445 * x*x + 0.1315 * x + 118.2	2,025779
Kubisch	y2 = 0,0001357 * x*x*x + -0,01404 * x*x + 0,5601 * x + 116,2	1,25766

Interessanterweise scheint das lineare Modell sogar besser zu passen, als das quadratische. Aber am besten sieht man das in der Visualisierung.

Abbildung 4: Zweiter Plot x gegen y2 mit den Regressions-Ergebnissen

Die Visualisierung zeigt, dass das lineare und das quadratische Modell, den Verlauf der Daten überhaupt nicht abschätzen können. Das kubische Modell erstellt eine annähernd passende Stufe, wobei die Stufe zu früh einsetzt und danach ein Überschwingen aufweist. Für größere Werte von x entfernt sich die kubische Kurve aber immer weiter von den Daten. Hier werden diese 3 Modelle bereits an ihre Grenzen geführt.

Die dritte Regression

Den folgenden Code in R habe ich in der Datei Regression3.r zusammengefasst.

Nach dem Anlegen der Vektoren x und y3 ergibt sich folgendes erstes Bild der Daten.

Abbildung 5: Erster Plot x gegen y3

Aus diesem Plot sieht man, dass man eigentlich eine Stufenfunktion benötigt. Einfache Regressionsmodelle werden hier keine sehr guten Ergebnisse liefern. Die maximalen Residiuen liegen hier bei 1,20735 (lineares Modell), 1,201945 (quadratisches Modell) und 1,389111 (kubisches Modell).

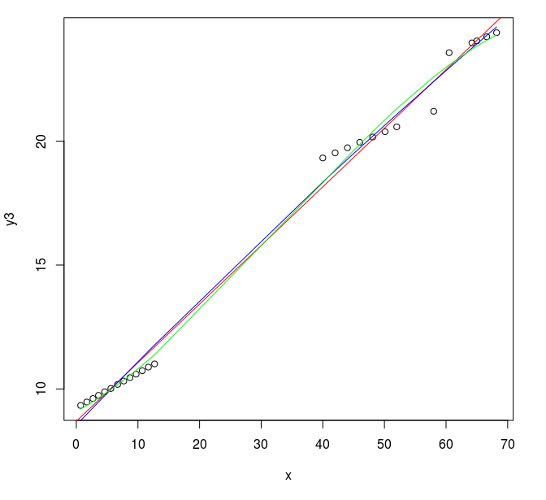
Abbildung 6: Zweiter Plot x gegen y3 mit den Regressions-Ergebnissen

Alle Modelle mitteln nur so gut wie möglich, die Abweichungen von einer geraden Steigung und berücksichtigen die Stufen in den Werten nicht.